It is known that the area under one hump of the sine wave is exactly $~2\,$; therefore we know that $\qquad \displaystyle \int_0^{\pi}\sin x\,dx=2~~$ and is equal to the area of the shaded region shown below. $\qquad$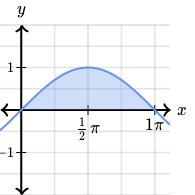 With this knowledge, evaluate each of the following. $~~~$(a)$~~~ \displaystyle \int_0^{\pi}3\sin x\,dx=$ [[☃ expression 1]] $~~~$(b)$~~~ \displaystyle \int_{\pi}^{\pi}3\sin x\,dx=$ [[☃ expression 2]] $~~~$(c)$~~~ \displaystyle \int_{-\pi}^{\pi}\big(\sin x+3\big)\,dx=$ [[☃ expression 3]]