Let $~I~$ be the blue shaded region between the graphs of
$\qquad f(x)=2-\dfrac12x~~~$and$~~~g(x)=\sqrt{\dfrac x2}$
and let $~II~$ be the red shaded region between the graph of
$\qquad ~~g(x)=\sqrt{\dfrac x2}~~$and the $~x$-axis for $~x\in[0,2]$
as shown in the figure.
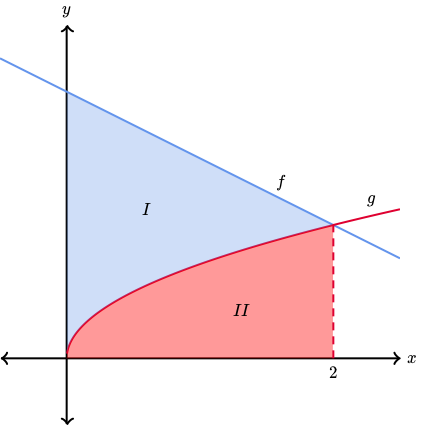
**Match each region with the definite integral that gives its area.**
[[☃ matcher 1]]